 1239
1239
Bitcoin is een cryptocurrency. Dat is voor de gemiddelde lezer waarschijnlijk niets nieuws, maar wat betekent dat eigenlijk? Crypto doelt op cryptografie, wat klinkt als iets dat complex en moeilijk is. In dit artikel duiken we wat verder in deze cryptografie: het ECDSA.
Bitcoin betaling
Om het nut en doel van de cryptografie te begrijpen, is het goed om te snappen hoe een bitcoin transactie werkt. Als je een betaling doet, moet je voldoen aan een aantal voorwaarden. Je doet dit vanuit je eigen wallet, waar jij als het goed is als enige toegang tot hebt. Deze toegang verkrijg je door aan te tonen dat jij de private key hebt.
Als je BTC verstuurt, doe je dit naar een wallet adres van de ontvanger. Dit wallet adres hoort bij een public key. Iedereen die Bitcoin gebruikt heeft een eigen key pair. Dit slaat op een stukje code die nodig is om óf Bitcoin te versturen óf om Bitcoin te ontvangen.
Bij dit stukje code komt cryptografie kijken.
Cryptografie
Cryptografie is de tak in de wiskunde waarmee we wiskundige bewijzen kunnen maken met een enorm hoge security. Online commerce en bankieren maken al gebruik van cryptografie.
In het geval van Bitcoin wordt cryptografie gebruikt om het voor iemand onmogelijk te maken om geld uit een wallet van een andere gebruiker te versturen. Het kan ook worden gebruikt om een wallet te versleutelen, zodat deze niet zonder wachtwoord kan worden gebruikt.
Een private key is een speciaal stukje data dat aantoont dat jij de rechten hebt een digitale handtekening te zetten. Zo'n cryptographic signature is als het ware een stukje wiskundige magie dat laat zien dat een wallet en een private key bij elkaar horen.
Maar kun je dit niet raden, zoals een pincode te raden is?
Algoritme
Het algoritme dat Bitcoin hiervoor gebruikt heet de ECDSA. Dit staat voor Elliptic Curve Digital Signature Algorithm. Dit algoritme zorgt voor een aantal dingen.
De private key is een geheim en random 'nummer' dat iemand genereert. Het is een unsigned 256 bit integer van 32 bytes. Dit getal correspondeert met een public key. Deze public key kan 'berekend' worden vanaf deze private key, maar vice versa kan het niet. En de manier hoe deze private key correspondeert, is complex.
Zie het als een biljarttafel. Je kunt niet berekenen of terughalen hoe de ballen de vorige ronde lagen als je alleen de huidige situatie hebt zoals die voor iedereen te zien is (public key). Toch kan degene die de beurt heeft gespeeld (met de private key) aantonen dat hij de ballen heeft gestoten door alles exact op de nanometer te reconstrueren zoals het er vóór de stoot uit zag.
Of een ander voorbeeld: een ei kun je wel koken, maar niet 'ontkoken' waardoor het weer vloeibaar wordt. In de wiskunde kun je dit soort trucjes ook toepassen.
Er zijn verschillende soorten ECDSA's. Het is afhankelijk van het type parameters dat je in zo'n algoritme stopt. Bij Bitcoin is dat Secp256k1. Doordat we met ons allen deze parameter gebruiken, komt het algoritme neer op een formule die er als volgt uit ziet: y2 = x3 + 7. Deze formule zorgt op zijn beurt weer voor een curve.
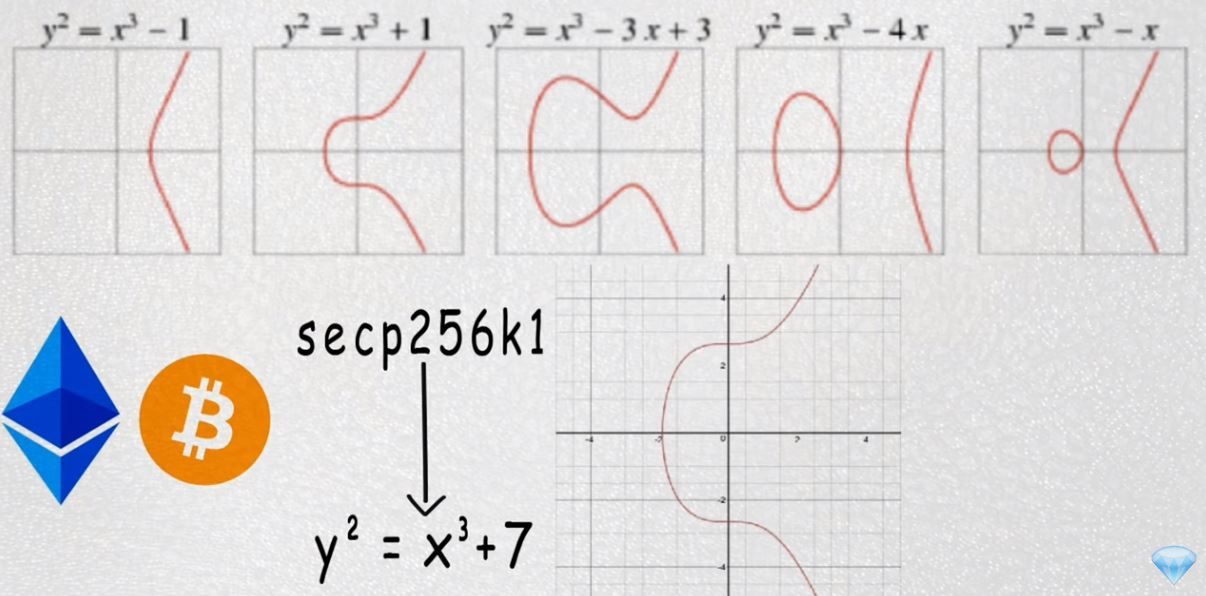
Allemaal leuk en aardig zo'n grafiekje, maar hoe heeft dit te maken met een key pair? Het komt op het volgende neer. Op de curve kun je gigantisch en ontelbaar veel punten zetten. Als je hier een lijn doorheen trekt, kruist die de curve op een andere coördinaat. Zo krijg je nieuwe punten op dezelfde curve, ook wel point doubling en point addition genoemd.
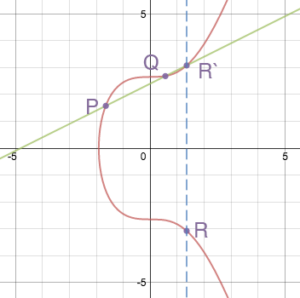
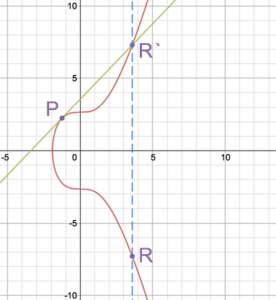
Dit kun je aantal keren doen ieder nieuw punt dat op de lijn ontstaat, krijg je steeds meer mogelijke combinaties. Maar vind dan maar eens het juiste geheime getal waarbij je moet stoppen.
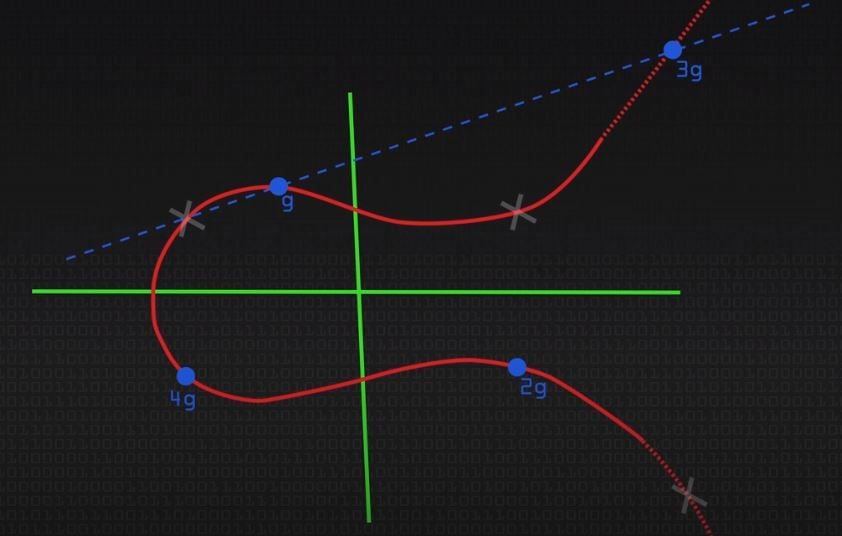
Iedere nieuw punt krijgt een naam: g, 2g, 3g, 4g et cetera. Maar wat als ik een random punt op deze lijn zet en wil weten welke g dat is, dan is dat onmogelijk te raden. Het kan een 295039473g zijn maar misschien is het ook wel 348034834g. En dit is precies het geheime nummer, de private key.
Je kunt dus een boodschap wegsturen met een openstaande variabele die alleen jij kunt invullen. En deze variabele (g) moet zó exact zijn dat het onmogelijk is om deze goed te gokken om het corresponderende punt op de curve te vinden die nodig is om een boodschap te signeren. In onderstaande video legt Computerphile het uit:
De gegenereerde variabele is de random gegenereerde private key. Hierbij hoort dus een public key, maar het terug te herleiden is onmogelijk. Hierdoor is én jouw Bitcoin veilig én kun je toch een public key versturen.
Hou je van wiskunde? Lees dan deze uitleg van core developer Pieter Wuille op Stackexchange.
Maar pas ook op: als jij jouw private key kwijt bent, kun je die dus niet herstellen. Het zijn van je eigen bank brengt dus ook verantwoordelijkheden met zich mee.













